Mesure de l'inductance synchrone des moteurs à aimants permanents

I. Le but et l'importance de la mesure de l'inductance synchrone
(1) Objectif de la mesure des paramètres de l'inductance synchrone (c'est-à-dire l'inductance transversale)
Les paramètres d'inductance AC et DC sont les deux paramètres les plus importants dans un moteur synchrone à aimant permanent. Leur acquisition précise est la condition préalable et la base du calcul des caractéristiques du moteur, de la simulation dynamique et du contrôle de la vitesse. L'inductance synchrone peut être utilisée pour calculer de nombreuses propriétés en régime permanent telles que le facteur de puissance, le rendement, le couple, le courant d'induit, la puissance et d'autres paramètres. Dans le système de contrôle du moteur à aimant permanent utilisant le contrôle vectoriel, les paramètres de l'inducteur synchrone sont directement impliqués dans l'algorithme de contrôle, et les résultats de la recherche montrent que dans la région magnétique faible, l'imprécision des paramètres du moteur peut entraîner une réduction significative du couple. et le pouvoir. Cela montre l'importance des paramètres de l'inducteur synchrone.
(2) Problèmes à noter lors de la mesure de l'inductance synchrone
Afin d'obtenir une densité de puissance élevée, la structure des moteurs synchrones à aimants permanents est souvent conçue pour être plus complexe et le circuit magnétique du moteur est plus saturé, ce qui fait que le paramètre d'inductance synchrone du moteur varie avec la saturation de le circuit magnétique. En d'autres termes, les paramètres changeront avec les conditions de fonctionnement du moteur, et les conditions de fonctionnement nominales des paramètres d'inductance synchrone ne peuvent pas refléter avec précision la nature des paramètres du moteur. Il est donc nécessaire de mesurer les valeurs d’inductance dans différentes conditions de fonctionnement.
2. méthodes de mesure de l'inductance synchrone du moteur à aimant permanent
Cet article rassemble diverses méthodes de mesure de l'inductance synchrone et en fait une comparaison et une analyse détaillées. Ces méthodes peuvent être grossièrement classées en deux types principaux : le test de charge direct et le test statique indirect. Les tests statiques sont divisés en tests statiques AC et tests statiques DC. Aujourd'hui, le premier volet de nos « Méthodes de test d'inductance synchrone » expliquera la méthode de test de charge.

La littérature [1] introduit le principe de la méthode de chargement direct. Les moteurs à aimants permanents peuvent généralement être analysés en utilisant la théorie de la double réaction pour analyser leur fonctionnement en charge, et les diagrammes de phases du fonctionnement du générateur et du moteur sont présentés dans la figure 1 ci-dessous. L'angle de puissance θ du générateur est positif lorsque E0 dépasse U, l'angle du facteur de puissance φ est positif lorsque I dépasse U et l'angle du facteur de puissance interne ψ est positif lorsque E0 dépasse I. L'angle de puissance θ du moteur est positif avec U dépassant E0, l'angle du facteur de puissance φ est positif lorsque U dépasse I et l'angle du facteur de puissance interne ψ est positif lorsque I dépasse E0.

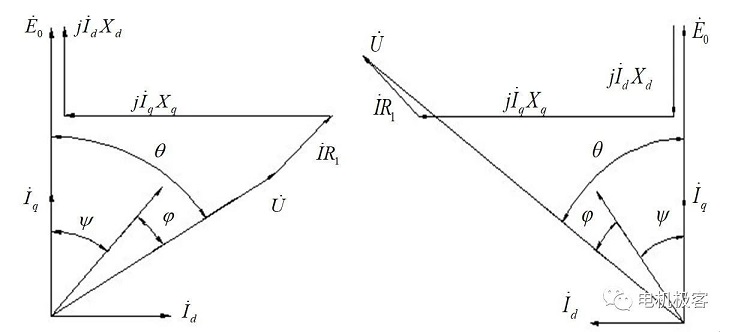
Fig. 1 Diagramme de phases du fonctionnement d'un moteur synchrone à aimant permanent
(a) État du générateur (b) État du moteur

Selon ce diagramme de phases, il est possible d'obtenir : lorsque le fonctionnement en charge du moteur à aimant permanent, la force électromotrice d'excitation à vide mesurée E0, la tension aux bornes de l'induit U, le courant I, l'angle du facteur de puissance φ et l'angle de puissance θ, etc., peuvent être obtenus. courant de l'axe droit, composante transversale Id = Isin (θ - φ) et Iq = Icos (θ - φ), alors Xd et Xq peuvent être obtenus à partir de l'équation suivante :

Lorsque le générateur est en marche :

Xd=[E0-Ucosθ-IR1cos(θ-φ)]/Id (1)
Xq=[Usinθ+IR1sin(θ-φ)]/Iq (2)

Lorsque le moteur tourne :

Xd=[E0-Ucosθ+IR1cos(θ-φ)]/Id (3)
Xq=[Usinθ-IR1sin(θ-φ)]/Iq (4)

Les paramètres d'état stable des moteurs synchrones à aimants permanents changent à mesure que les conditions de fonctionnement du moteur changent et lorsque le courant d'induit change, Xd et Xq changent. Par conséquent, lors de la détermination des paramètres, veillez également à indiquer les conditions de fonctionnement du moteur. (Quantité de courant d'arbre alternatif et direct ou de courant de stator et angle du facteur de puissance interne)

La principale difficulté lors de la mesure des paramètres inductifs par la méthode de charge directe réside dans la mesure de l'angle de puissance θ. Comme nous le savons, il s'agit de la différence d'angle de phase entre la tension aux bornes du moteur U et la force électromotrice d'excitation. Lorsque le moteur fonctionne de manière stable, la tension finale peut être obtenue directement, mais E0 ne peut pas être obtenu directement, elle ne peut donc être obtenue que par une méthode indirecte pour obtenir un signal périodique avec la même fréquence que E0 et une différence de phase fixe à remplacer. E0 afin de faire une comparaison de phase avec la tension finale.

Les méthodes indirectes traditionnelles sont :
1) dans la fente d'induit du moteur testé et de la bobine d'origine du moteur, plusieurs tours de fil fin comme bobine de mesure, afin d'obtenir la même phase avec l'enroulement du moteur sous le signal de comparaison de tension de test, par la comparaison de l'angle du facteur de puissance peut être obtenu.
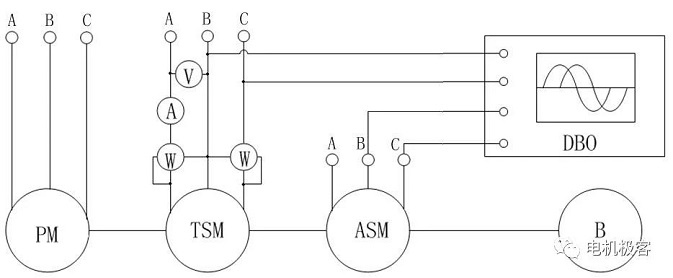
2) Installer un moteur synchrone sur l'arbre du moteur testé identique au moteur testé. La méthode de mesure de phase de tension [2], qui sera décrite ci-dessous, est basée sur ce principe. Le schéma de connexion expérimental est illustré à la figure 2. Le TSM est le moteur synchrone à aimant permanent testé, l'ASM est un moteur synchrone identique qui est en outre requis, le PM est le moteur principal, qui peut être soit un moteur synchrone, soit un moteur à courant continu. moteur, B est le frein et le DBO est un oscilloscope à double faisceau. Les phases B et C du TSM et de l'ASM sont connectées à l'oscilloscope. Lorsque le TSM est connecté à une alimentation triphasée, l'oscilloscope reçoit les signaux VTSM et E0ASM. parce que les deux moteurs sont identiques et tournent de manière synchrone, le potentiel arrière à vide du TSM du testeur et le potentiel arrière à vide de l'ASM, qui agit comme un générateur, E0ASM, sont en phase. Par conséquent, l'angle de puissance θ, c'est-à-dire la différence de phase entre VTSM et E0ASM, peut être mesuré.

Fig. 2 Schéma de câblage expérimental pour mesurer l'angle de puissance

Cette méthode n'est pas très couramment utilisée, principalement parce que : ① le petit moteur synchrone ou le transformateur rotatif monté sur l'arbre du rotor doit être mesuré. Le moteur a deux extrémités d'arbre étirées, ce qui est souvent difficile à faire. ② La précision de la mesure de l'angle de puissance dépend en grande partie du contenu harmonique élevé du VTSM et de l'E0ASM, et si le contenu harmonique est relativement important, la précision de la mesure sera réduite.
3) Pour améliorer la précision du test d'angle de puissance et la facilité d'utilisation, utilisez désormais davantage de capteurs de position pour détecter le signal de position du rotor, puis comparez les phases avec l'approche de la tension finale.
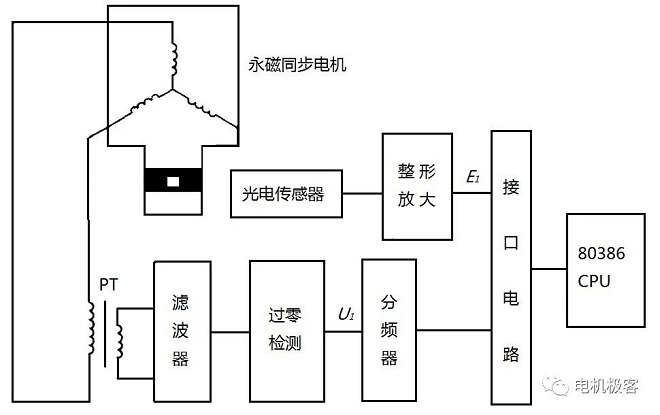
Le principe de base est d'installer un disque photoélectrique projeté ou réfléchi sur l'arbre du moteur synchrone à aimant permanent mesuré, le nombre de trous uniformément répartis sur le disque ou des repères noir et blanc et le nombre de paires de pôles du moteur synchrone testé . Lorsque le disque fait un tour avec le moteur, le capteur photoélectrique reçoit p signaux de position du rotor et génère p impulsions basse tension. Lorsque le moteur fonctionne de manière synchrone, la fréquence de ce signal de position du rotor est égale à la fréquence de la tension aux bornes de l'induit et sa phase reflète la phase de la force électromotrice d'excitation. Le signal d'impulsion de synchronisation est amplifié par mise en forme, déphasage et tension d'induit du moteur de test pour comparaison de phase afin d'obtenir la différence de phase. Réglé lorsque le moteur fonctionne à vide, la différence de phase est θ1 (environ à ce moment l'angle de puissance θ = 0), lorsque la charge fonctionne, la différence de phase est θ2, alors la différence de phase θ2 - θ1 est la valeur mesurée Valeur d'angle de puissance de charge du moteur synchrone à aimant permanent. Le diagramme schématique est présenté à la figure 3.

Fig. 3 Diagramme schématique de la mesure de l'angle de puissance

Comme dans le disque photoélectrique uniformément recouvert d'une marque noire et blanche, il est plus difficile, et lorsque les pôles du moteur synchrone à aimant permanent mesurés, le disque de marquage en même temps ne peut pas être commun les uns avec les autres. Par souci de simplicité, on peut également tester dans l'arbre d'entraînement du moteur à aimant permanent enveloppé dans un cercle de ruban noir, recouvert d'une marque blanche, la source de lumière du capteur photoélectrique réfléchissant émise par la lumière recueillie dans ce cercle sur la surface du ruban. De cette manière, à chaque tour du moteur, le capteur photoélectrique dans le transistor photosensible doit recevoir une lumière réfléchie et conductée une fois, ce qui entraîne un signal d'impulsion électrique, après amplification et mise en forme pour obtenir un signal de comparaison E1. à partir de l'extrémité de l'enroulement d'induit du moteur d'essai de toute tension biphasée, par le transformateur de tension PT jusqu'à une basse tension, envoyée au comparateur de tension, la formation d'un représentant de la phase rectangulaire du signal d'impulsion de tension U1. U1 par la fréquence de division p, la comparaison du comparateur de phase pour obtenir une comparaison entre la phase et le comparateur de phase. U1 par la fréquence de division p, par le comparateur de phase pour comparer sa différence de phase avec le signal.
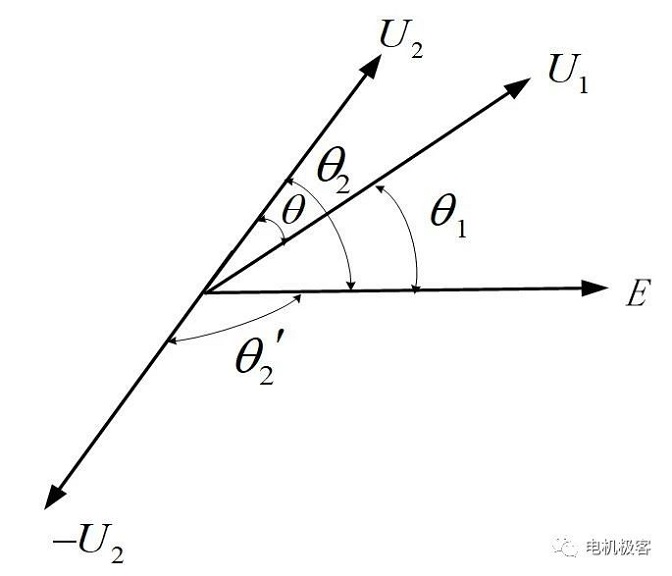
L'inconvénient de la méthode de mesure de l'angle de puissance ci-dessus est qu'il faut faire la différence entre les deux mesures pour obtenir l'angle de puissance. Afin d'éviter les deux quantités soustraites et de réduire la précision, dans la mesure de la différence de phase de charge θ2, l'inversion du signal U2, la différence de phase mesurée est θ2'=180 ° - θ2, l'angle de puissance θ=180 ° - ( θ1 + θ2'), qui convertit les deux quantités de la soustraction de la phase à l'addition. Le diagramme de quantité de phase est présenté sur la figure 4.

Fig. 4 Principe de la méthode d'addition de phase pour calculer la différence de phase

Une autre méthode améliorée n'utilise pas la division de fréquence du signal de forme d'onde rectangulaire de tension, mais utilise un micro-ordinateur pour enregistrer simultanément la forme d'onde du signal, respectivement, via l'interface d'entrée, enregistrer les formes d'onde du signal de tension à vide et de position du rotor U0, E0, ainsi que Les signaux de forme d'onde rectangulaires de tension de charge et de position du rotor U1, E1, puis déplacent les formes d'onde des deux enregistrements l'un par rapport à l'autre jusqu'à ce que les formes d'onde de deux signaux de forme d'onde rectangulaires de tension se chevauchent complètement, lorsque la différence de phase entre les deux rotors. la différence entre les deux signaux de position du rotor est l'angle de puissance ; ou déplacez la forme d'onde pour que les deux formes d'onde du signal de position du rotor coïncident, alors la différence de phase entre les deux signaux de tension est l'angle de puissance.
Il convient de souligner que lors du fonctionnement à vide réel du moteur synchrone à aimant permanent, l'angle de puissance n'est pas nul, en particulier pour les petits moteurs, en raison du fonctionnement à vide de la perte à vide (y compris la perte de cuivre du stator, la perte de fer, perte mécanique, perte parasite) est relativement importante, si vous pensez que l'angle de puissance à vide est nul, cela entraînera une erreur importante dans la mesure de l'angle de puissance, qui peut être utilisée pour faire fonctionner le moteur à courant continu dans l'état du moteur, le sens de la direction et le Test de direction du moteur cohérent, avec la direction du moteur à courant continu, le moteur à courant continu peut fonctionner dans le même état et le moteur à courant continu peut être utilisé comme moteur de test. Cela peut rendre le moteur à courant continu fonctionnant dans l'état du moteur, la direction et la direction du moteur de test cohérentes avec le moteur à courant continu pour fournir toutes les pertes d'arbre du moteur de test (y compris la perte de fer, la perte mécanique, la perte parasite, etc.). La méthode de jugement est que la puissance d'entrée du moteur de test est égale à la consommation de cuivre du stator, c'est-à-dire P1 = pCu, ainsi qu'à la tension et au courant en phase. Cette fois, le θ1 mesuré correspond à l’angle de puissance nul.
Résumé : les avantages de cette méthode :
① La méthode de charge directe peut mesurer l'inductance de saturation en régime permanent dans divers états de charge et ne nécessite pas de stratégie de contrôle, intuitive et simple.
La mesure étant effectuée directement sous charge, l'effet de saturation et l'influence du courant de démagnétisation sur les paramètres d'inductance peuvent être pris en compte.
Inconvénients de cette méthode :
① La méthode de charge directe doit mesurer plus de quantités en même temps (tension triphasée, courant triphasé, angle du facteur de puissance, etc.), la mesure de l'angle de puissance est plus difficile et la précision du test de chaque quantité a un impact direct sur la précision des calculs des paramètres, et toutes sortes d'erreurs dans le test des paramètres sont faciles à accumuler. Par conséquent, lors de l’utilisation de la méthode de charge directe pour mesurer les paramètres, il convient de prêter attention à l’analyse des erreurs et de sélectionner une précision plus élevée de l’instrument de test.
② La valeur de la force électromotrice d'excitation E0 dans cette méthode de mesure est directement remplacée par la tension aux bornes du moteur à vide, et cette approximation entraîne également des erreurs inhérentes. Parce que le point de fonctionnement de l'aimant permanent change avec la charge, ce qui signifie qu'à différents courants statoriques, la perméabilité et la densité de flux de l'aimant permanent sont différentes, donc la force électromotrice d'excitation résultante est également différente. De cette manière, il n’est pas très précis de remplacer la force électromotrice d’excitation en condition de charge par la force électromotrice d’excitation sans charge.
Références
[1] Tang Renyuan et coll. Théorie et conception modernes des moteurs à aimants permanents. Pékin : Presse de l'industrie des machines. Mars 2011
[2] JF Gieras, M. Wing. Technologie, conception et applications des moteurs à aimant permanent, 2e éd. New York : Marcel Dekker, 2002 : 170~171
Copyright : Cet article est une réimpression du aperçu du moteur du numéro public WeChat (电机极客), le lien originalhttps://mp.weixin.qq.com/s/Swb2QnApcCWgbLlt9jMp0A

Cet article ne représente pas le point de vue de notre entreprise. Si vous avez des opinions ou des points de vue différents, veuillez nous corriger !